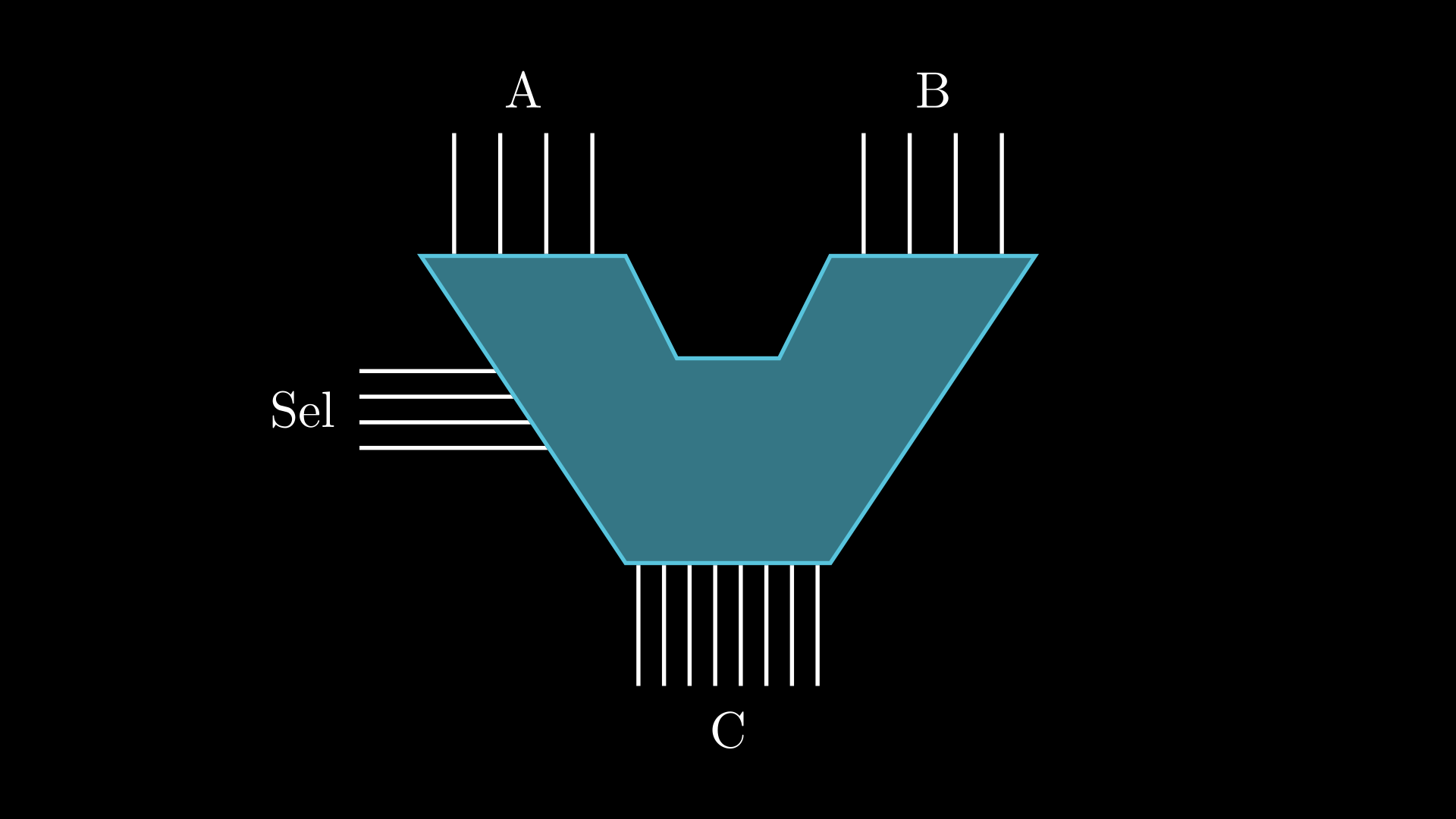
ALU
Problema
Queremos diseñar un circuito combinacional que tenga la siguiente funcion: recibir un selector de 4 bits, dos entradas de n bits y dar una salida de 2n bits donde dependiendo el selector se escoga una operación artimética o lógica que se lleve a cabo a partir de los dos operandos de entrada, a este circuito se le conoce como ALU (Unidad Aritmética Lógica), se clasifican por las operaciones que puede llevar a cabo y el tamaño de sus operandos, en el ejemplo de la figura 1 tenemos un ALU de operandos de 4 bits, un selector de 4 bits y una salida de 8 bits que es capaz de realizar las siguientes operciones:
- Pasar "a"
- a + 1
- a - 1
- Pasar "b"
- b + 1
- b - 1
- a+b
- a*b
- a/b
- a negada
- b negada
- a AND b
- a OR b
- a NAND b
- a NOR b
Para crear este circuito podemos hacerlo mediante mapas de Karnaugh o tablas de verdad y de esa forma encontraríamos la ecuación lógica que lo describe, pero ya que sabemos que hoy en día podemos hacer uso de herramientas CAD para facilitar este proceso, procederé a mostrar directamente su implementación en los HDL's.
Descripción del Circuito
AHDL
Implementación de un ALU en AHDL.
INCLUDE "lpm_divide";
SUBDESIGN ALU(
a[3..0], b[3..0], sel[3..0] : INPUT;
z[7..0] : OUTPUT;
)
VARIABLE
u1 : lpm_divide WITH (LPM_WIDTHN = 4, LPM_WIDTHD = 4, LPM_NREPRESENTATION = "SIGNED", LPM_DREPRESENTATION = "SIGNED");
quo[3..0] : NODE;
BEGIN
u1.numer[] = a[];
u1.denom[] = b[];
quo[] = u1.quotient[];
CASE (sel[]) IS
WHEN 0 => z[] = (a[3], a[3], a[3], a[3], a[]);
WHEN 1 => z[] = (a[3], a[3], a[3], a[3], a[])+1;
WHEN 2 => z[] = (a[3], a[3], a[3], a[3], a[])-1;
WHEN 3 => z[] = (b[3], b[3], b[3], b[3], b[]);
WHEN 4 => z[] = (b[3], b[3], b[3], b[3], b[])+1;
WHEN 5 => z[] = (b[3], b[3], b[3], b[3], b[])-1;
WHEN 6 => z[] = (a[3], a[3], a[3], a[3], a[])+(b[3], b[3], b[3], b[3], b[]);
WHEN 7 => z[] = (a[3], a[3], a[3], a[3], a[])*(b[3], b[3], b[3], b[3], b[]);
WHEN 8 => z[] = (quo[3], quo[3], quo[3], quo[3], quo[]);
WHEN 9 => z[] = (!a[3], !a[3], !a[3], !a[3], !a[]);
WHEN 10 => z[] = (!b[3], !b[3], !b[3], !b[3], !b[]);
WHEN 11 => z[] = (b"0000000", ((a[0]&b[0])&(a[1]&b[1]))&((a[2]&b[2])&(a[3]&b[3])));
WHEN 12 => z[] = (b"0000000", ((a[0]#b[0])#(a[1]#b[1]))#((a[2]#b[2])#(a[3]#b[3])));
WHEN 13 => z[] = (b"0000000", !(((a[0]&b[0])&(a[1]&b[1]))&((a[2]&b[2])&(a[3]&b[3]))));
WHEN 14 => z[] = (b"0000000", !(((a[0]#b[0])#(a[1]#b[1]))#((a[2]#b[2])#(a[3]#b[3]))));
WHEN OTHERS => z[] = b"XXXXXXXX";
END CASE;
END;VHDL
Implementación de un ALU en VHDL.
LIBRARY ieee;
LIBRARY lpm;
USE ieee.std_logic_1164.all;
USE ieee.std_logic_signed.all;
USE lpm.lpm_components.all;
ENTITY ALU IS
PORT(a, b : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
sel : IN INTEGER RANGE 0 TO 15;
z : OUT STD_LOGIC_VECTOR(7 DOWNTO 0));
END ALU;
ARCHITECTURE Behaviour OF ALU IS
SIGNAL quo : STD_LOGIC_VECTOR(3 DOWNTO 0);
BEGIN
u1 : lpm_divide GENERIC MAP(LPM_WIDTHN => 4, LPM_WIDTHD => 4, LPM_NREPRESENTATION => "SIGNED", LPM_DREPRESENTATION => "SIGNED") PORT MAP(NUMER => a, DENOM => b, QUOTIENT => quo);
PROCESS(a,b,sel)
BEGIN
CASE (sel) IS
WHEN 0 => z <= (a(3) & a(3) & a(3) & a(3) & a);
WHEN 1 => z <= (a(3) & a(3) & a(3) & a(3) & a)+1;
WHEN 2 => z <= (a(3) & a(3) & a(3) & a(3) & a)-1;
WHEN 3 => z <= (b(3) & b(3) & b(3) & b(3) & b);
WHEN 4 => z <= (b(3) & b(3) & b(3) & b(3) & b)+1;
WHEN 5 => z <= (b(3) & b(3) & b(3) & b(3) & b)-1;
WHEN 6 => z <= (a(3) & a(3) & a(3) & a(3) & a)+(b(3) & b(3) & b(3) & b(3) & b);
WHEN 7 => z <= a*b;
WHEN 8 => z <= (quo(3) & quo(3) & quo(3) & quo(3) & quo);
WHEN 9 => z <= (NOT a(3) & NOT a(3) & NOT a(3) & NOT a(3) & NOT a);
WHEN 10 => z <= (NOT b(3) & NOT b(3) & NOT b(3) & NOT b(3) & NOT b);
WHEN 11 => z <= ("0000000" & (((a(0) AND b(0))AND(a(1) AND b(1)))AND((a(2) AND b(2))AND(a(3) AND b(3)))));
WHEN 12 => z <= ("0000000" & (((a(0) OR b(0))OR(a(1) OR b(1)))OR((a(2) OR b(2))OR(a(3) OR b(3)))));
WHEN 13 => z <= ("0000000" & (NOT(((a(0) AND b(0))AND(a(1) AND b(1)))AND((a(2) AND b(2))AND(a(3) AND b(3))))));
WHEN 14 => z <= ("0000000" & (NOT(((a(0) OR b(0))OR(a(1) OR b(1)))OR((a(2) OR b(2))OR(a(3) OR b(3))))));
WHEN OTHERS => z <= "XXXXXXXX";
END CASE;
END PROCESS;
END Behaviour;Verilog
Implementación de un ALU en Verilog.
module ALU(a, b, sel, z);
input [3:0] a, b, sel;
output reg [7:0] z;
wire [3:0]quo;
lpm_divide #(.lpm_widthn(4), .lpm_widthd(4), .lpm_nrepresentation("SIGNED"), .lpm_drepresentation("SIGNED")) u1 (.quotient(quo), .numer(a), .denom(b));
always @(a, b, sel)
case(sel)
0 : z = {{4{a[3]}}, a};
1 : z = {{4{a[3]}}, a}+1;
2 : z = {{4{a[3]}}, a}-1;
3 : z = {{4{b[3]}}, b};
4 : z = {{4{b[3]}}, b}+1;
5 : z = {{4{b[3]}}, b}-1;
6 : z = {{4{a[3]}}, a}+{{4{b[3]}}, b};
7 : z = {{4{a[3]}}, a}*{{4{b[3]}}, b};
8 : z = {{4{quo[3]}}, quo};
9 : z = {~a[3], ~a[3], ~a[3], ~a[3], ~a};
10 : z = {~b[3], ~b[3], ~b[3], ~b[3], ~b};
11 : z = {7'b0000000, {{{a[0]&b[0]}&{a[1]&b[1]}}&{{a[2]&b[2]}&{a[3]&b[3]}}}};
12 : z = {7'b0000000, {{{a[0]|b[0]}|{a[1]|b[1]}}|{{a[2]|b[2]}|{a[3]|b[3]}}}};
13 : z = {7'b0000000, ~{{{a[0]&b[0]}&{a[1]&b[1]}}&{{a[2]&b[2]}&{a[3]&b[3]}}}};
14 : z = {7'b0000000, ~{{{a[0]|b[0]}|{a[1]|b[1]}}|{{a[2]|b[2]}|{a[3]|b[3]}}}};
default : z = 8'bXXXXXXXX;
endcase
endmodule